1. tuning curve 绘制
1.1 baseline
要求:对于数据集中的每一个神经元,使用一族参数化的曲线拟合其发放率随运动方向变化的关系。
对于一个二维的运动轨迹,所使用的参数化轨迹应该是余弦曲线。这一观点在Neuronal Population Coding of Movement Direction中提出。用单位向量$\boldsymbol{m}$表示运动方向,则应该有
$$
d(\boldsymbol{m})=b+b_x\boldsymbol{m}_x+b_y\boldsymbol{m}_y+b_z\boldsymbol{m}_z=b+(b_x, b_y, b_z)\cdot \boldsymbol{m}
$$
其中$d(\boldsymbol{m})$为某个神经元的发放率,$b, b_x, b_y, b_z$为参数。显然,这个模型下存在运动方向$(b_x, b_y, b_z)$使得发放率达到唯一的最大值。利用神经元的偏好方向,将公式重写为
$$
d(\boldsymbol{m})=b+k\cos(\theta_{CM})
$$
其中$\theta_{CM}$为运动方向和神经元偏好方向的夹角,$b,k$为参数。此为上课时提到的余弦形式 tuning curve 和线性拟合时间的关系。
综上,绘制 tuning curve 的基本步骤为:
- 确定一个 bin,将实验的时间区间划分为若干个 bin;
- 将运动数据和神经数据划分到对应的 bin 中;
- 对每一个 bin,通过起始时间和终止时间时光标的位置计算出光标的速度,正规化之后得到该区间对应的运动方向向量;
- 对每一个 bin,统计某一神经元在该区间内发放的次数;
- 对以上两个数据进行线性回归,计算$R^2$;
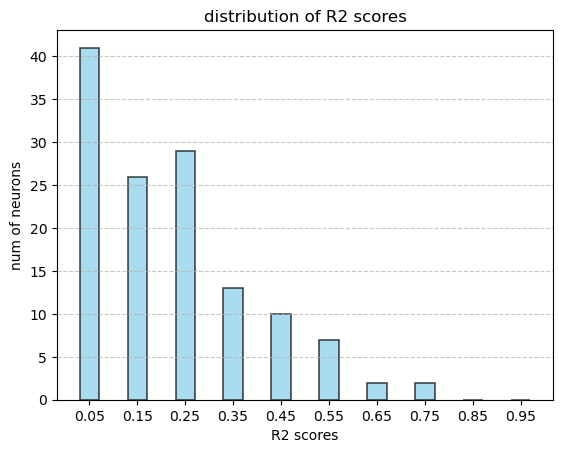
- 对所有神经元执行以上的操作,画出$R^2$的分布。
1.2 额外的数据处理
1.2.1 去除发放次数过低的神经元
baseline 获得的结果中会有很多$R^2=1$的神经元。实际上,这些神经元发放率过低,导致在使用 bin 之后非零的数据点极少,即使只是线性回归也能穿过这些点。这些数据可能只是噪声,而不是真实的神经元。因此,在计算时对神经元设置阈值,不允许发放次数过少的神经元参与计算。实际使用的阈值为300次。
for channel_id, channel in enumerate(data['spikes']):
for i, neuron in enumerate(channel):
if i == 0:
continue
spikes = neuron.flatten()
if len(spikes) < spike_num_threshold:
continue
去除这些数据之后,$R^2$开始表现出和课件上相似的分布趋势。只是$R^2$的值似乎太低了,大部分的$R^2$值都在0.2以下。
1.2.2 对角度划分 bin
观察光标的运动过程可以发现,光标的运动方向一直在发生一定范围的变化,并且神经元的发放率也不是那么稳定,即使大致在同一个方向上,发放率也会发生较大幅度的变化。这导致虽然使用瞪眼法可以看出在某一个大致的运动方向上,发放率的总体表现有明显的增强,但实际记录的数据中,有可能出现角度偏离一点点之后产生的数据点发放率就变成零的情况。这对于拟合并不是很友好。
为了对抗这种类型的噪声,参考之前的学长留下的代码,对角度划分一定数量的 bin。对 bin 范围内的脉冲发放数进行累加,每个 bin 用其中心的角度值代表。这样得到的数据分布呈现出更明显的趋势。
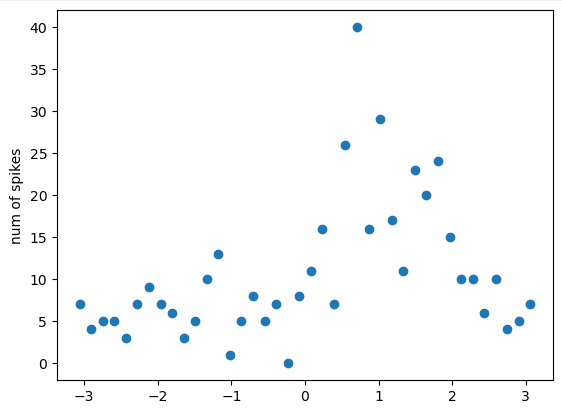
1.2.3 去除光标无明显移动的时间段
将数据可视化之后,可以发现实际上有相当大的一部分时间里,光标在到达目标之后等待下一个目标的出现。这个时间段中,光标没有明显的移动意图和趋势,计算得到的运动方向会剧烈变化,此时得到的数据未必是有意义的(个人猜测)。对每一个时间点,以过去的一段时间考虑,如果位移小于一定的阈值,则认为光标没有实际移动,不划分在被计算的时间段中。实际上这样做的效果并不明显,但仍然保留这部分算法。
1.3 结果
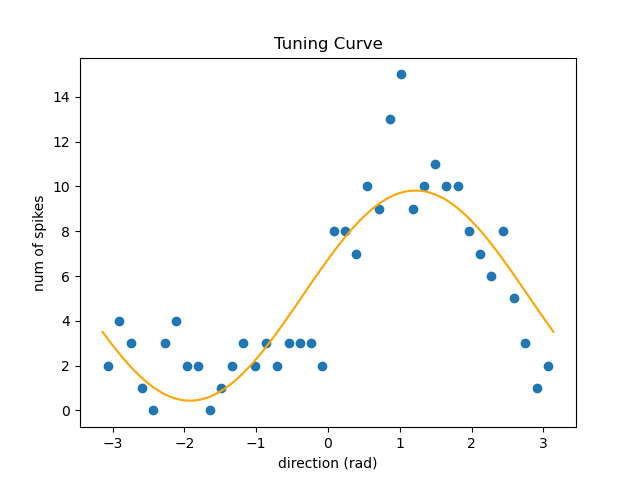
一个拟合得比较好的曲线是这样的。下面这个曲线的 $R^2$ 超过 0.7。
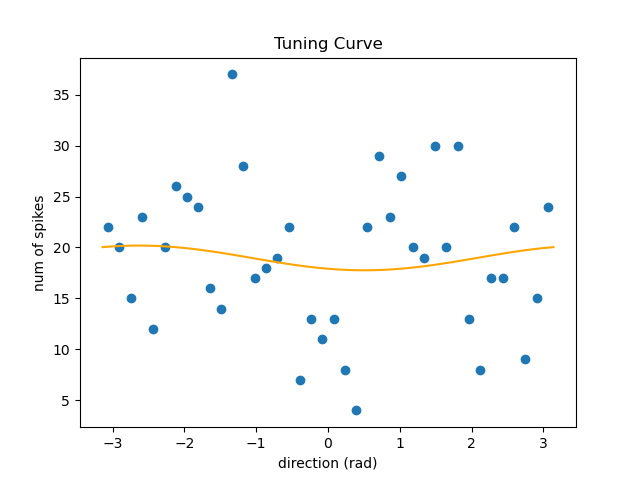
大部分还是拟合得很差的。下面的 $R^2$ 只有 0.01 左右。
2. 运动数据解码
2.1 Kalman Filter 实现的方式
使用 Kalman Filter 最主要的问题就是:如何确定状态转移矩阵和测量矩阵,以及如何确定系统噪声和测量噪声的方差?
上课的课件中提供了一种建模状态转移矩阵的方式,没有给出测量矩阵的建模方式。根据这个实验项目以及这篇论文,建模状态转移矩阵和测量矩阵更直接的方式是直接使用线性回归。以状态转移矩阵为例,实际上希望得到的效果是:
$$
X_{t+1}\approx AX_t, \qquad t=1, 2, ..., n-1
$$
定义损失为
$$
\mathcal{L}=\sum\parallel X_{t+1}-AX_t\parallel^2=\parallel X_{2:n}-X_{1:n-1}A\parallel^2.
$$
从而形成一个平凡的线性回归问题。测量矩阵是类似的。
对于系统噪声和测量噪声的方差,我参考了这个实验项目的实现,数学上相当于使用训练数据中的噪声来估计协方差矩阵。对系统噪声的估计为
$$
\begin{aligned}
e&=X_{2:n}-X_{1:n-1}A,\\
P&=e^T e.
\end{aligned}
$$
对观察噪声的估计类似。拟合时发现这两个协方差矩阵的估计对最终的表现影响很大,这种方式是尝试中效果最好的。
2.2 Linear Regression
第二种方式为直接使用线性回归。即直接将神经元的活动线性映射到运动数据上。
2.3 Linear Filter
第三种方式在这篇论文中提到。核心思想是当前时刻的运动可能不仅受到当前时刻(附加一个延迟)的神经活动的控制,可能还受到过去一定时段内的神经活动的控制。直觉上,用当前时刻与往前一个固定时间窗内的所有神经数据预测当前时刻的运动,效果应该会更好。
这种方式本质上还是在做线性拟合,方法不再赘述。
2.4 额外的数据处理
2.4.1 延迟
以上的参考资料中,均提到神经元的活动对运动的影响存在一定的延迟,实际上对 $firing\_rate_{t-\tau}$ 和 $motion_{t}$ 之间进行拟合能够获得更好的效果。为了实现方便,这里对运动数据进行了 2 个 bin 的延迟。添加延迟对拟合效果有较大的改善。
res = model.fit(spike_norm[:-bin_delay], motion[bin_delay:])
res.score(spike_norm[:-bin_delay], motion[bin_delay:])
2.4.2 运动数据的选择
预测目标选择为 $[x, y, v_x, v_y]$ 的效果要比 $[v_x, v_y]$ 要来得好。我也不知道为什么,但是实验结果就是这样()
2.4.3 PCA
这个实验项目中提到对神经元发放的数据进行了主成分分析,并保留一定的主成分用于测量矩阵的线性回归。这样做是合理的,因为直觉上通过特征并不多的运动数据预测上百个神经元的发放行为很难做到,神经元之间可能也存在一定的共线性。实际上,拟合测量矩阵时得到的 $R^2$ 值也非常低。但实验中发现 PCA 的效果并不好,甚至比使用原始的数据还差,因此没有保留。
2.5 结果
2.5.1 指标
按照要求,需要计算 $R^2$,CC(Pearson 相关系数)和 RMSE 三种指标。由于输出的是多维数据,三种指标都对每一个运动数据分别计算,然后取平均。
取时间 bin 为 0.1s,Linear Filter 的历史窗口为 5 个 bin(0.5s),运动数据和神经数据之间的延迟为 2 个 bin(0.2s),测试拟合效果。
| $R^2$ | RMSE | Correlation Coefficient | |
|---|---|---|---|
| Linear Regression | 0.385 | 40.209 | 0.619 |
| Kalman Filter | 0.499 | 39.305 | 0.732 |
| Linear Filter | 0.683 | 30.692 | 0.827 |
可以看到 Kalman Filter 的效果比纯粹的线性拟合确实要好。另外,比较意外的是 Linear Filter 是最简单有效的做法。但实际上这也是合理的,因为 Linear Filter 所具有的参数要比另外两者更多。
2.5.2 可视化
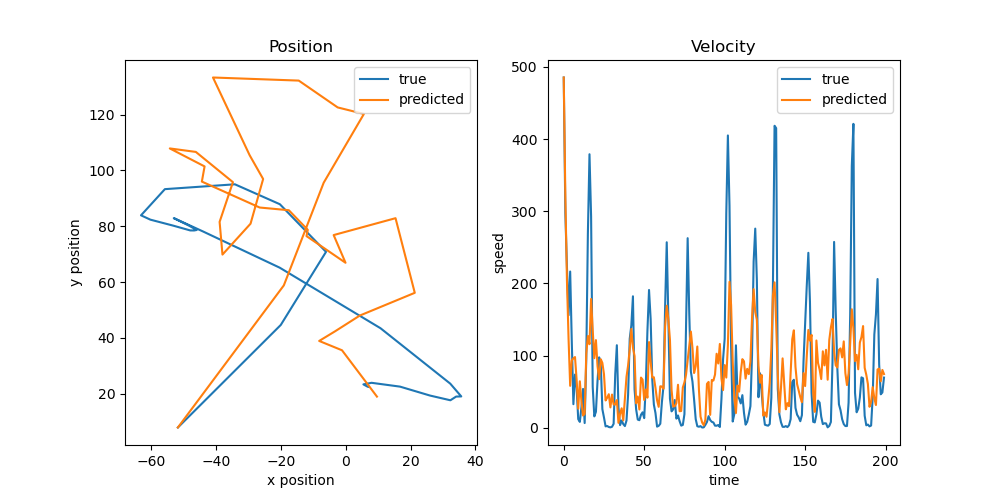
下图为使用 Kalman Filter 预测的运动轨迹和运动速度与真实情况的对比。可以看到,Kalman Filter 对方向的预测还是比较准确的,但是对于绝对位置还是偏离得比较严重。(大概率是还有一些其他的数据处理手段)
2.5.3 bin 的大小对解码的影响
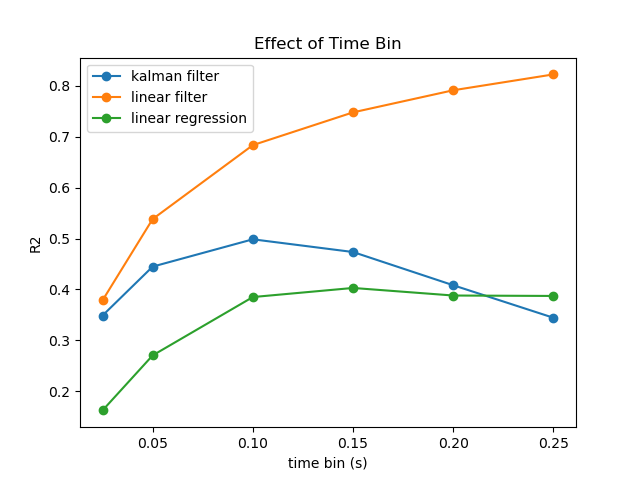
Kalman Filter 在 0.1s 左右的时间窗达到最优效果。其他的方法随着窗口长度的增加而提升性能,最终收敛到一个较稳定的值。
3. 总结
总体来说,$R^2$分布的结果看起来比较正常,后面的运动解码部分表现也还算合理,指标上可能差强人意。实际上,运动解码部分可能还有一些数据处理的手段可以调整,但是写到这里的时候已经做了五天了,有点干不动了。就先这样吧。






Comments NOTHING