主要的依据是这篇文章。阅读的主要目的是明白 Variational Inference 到底是怎么用法,什么时候用。有关 VAE 的说法实在是太多了,几乎有无数的理解角度,这里选了一种比较严谨的。文章是 arxiv 上的,引用量比较大的一篇从 lecture 改编来的教程。
Variational Inference 变分推断
变分推断没有一个很固定的形式。经典地来说,是下面这个问题:
有一个潜在变量$z$,以及相关的可观测变量$x$。我们知道$p(z)$以及条件分布$p(x|z)$,自然也知道它们的联合分布$p(z, x)$。在给定$x=D$的条件下,如何求出$p(z|x)$?
这问题看上去莫名其妙的,但在 VI 被使用的地方确实经常出现这样的需求。比如 VAE 中,我们假定了$z \sim \mathcal N(0, I)$,$x|z$也是高斯分布。至于为什么需要知道后验分布,之后再说。
第一个粗暴的想法就是,按照贝叶斯公式,
$$
p(z|x) = \frac{p(x|z)p(z)}{p(x)}
$$
但是这样的话,我们需要求$p(x)=\int_z p(x|z)p(z)dz$。可能遇到的两个问题是:
- 它很可能没有解析解。
- 如果进行数值求解,使用$p(x) \approx \frac{1}{N} \sum_i p(x|z_i)p(z_i)$求解,可能在较高维的空间中需要较多的采样次数。
总结起来,直接求解的计算代价太高。实际上并不是“无法计算”,只是代价太大了。
#question 关于数值求解的困难,P7 的位置给出了另一个解释。目前没看懂。
VI 的核心思想是使用一个简单的分布$q(z|x)$来逼近$p(z|x)$。由于被优化的对象是$q$,所以称为变分推断。
核心的步骤就是求它们之间的 KL 散度:
$$
\begin{aligned} \text{KL}(q(z|x) \parallel p(z|x)) &= \mathbb{E}_{z \sim q(z|x)} \left[ \log \frac{q(z|x)}{p(z|x)} \right] \\ &= \mathbb{E}_{z \sim q(z|x)} \left[ \frac{q(z|x) p(x)}{p(z, x)} \right] \\ &= \mathbb{E}_{z \sim q(z|x)} \left[ \frac{q(z|x)}{p(z, x)} \right] + \log(p(x)) \end{aligned}
$$
这里都是在$x=D$的条件下进行的。$x$是一个常量。
将上面的式子进行一个变换,得到
$$
\text{KL}(q(z|x) \parallel p(z|x)) = -\mathbb{E}_{z \sim q(z|x)} \left[ \frac{p(z, x)}{q(z|x)} \right] + \log(p(x)) \geq 0
$$
令$\text{ELBO}:=\mathbb E_{z \sim q(z|x)}\left[ \frac{p(z,x)}{q(z|x)} \right]$。观察到 KL 散度总是正的,$\log p(x)$总是负的,那么一定有$\text{ELBO}<=\log p(x)$。RHS 在贝叶斯推断中称为证据(evidence),因此前者被称为证据下界(Evidence Lower Bound, ELBO)。对于同一个$x=D$而言,证据是不变的,因此最小化 KL 散度就等同于最大化 ELBO。ELBO 一般是可计算的,从而把一个后验分布的求解转换成了优化问题。 #theorem
$\text{KL}(q(z|x)\parallel p(z|x))=-\text{ELBO}+\log p(x)$,其中$$
\text{ELBO}:=\mathbb E_{z \sim q(z|x)}\left[ \frac{p(z,x)}{q(z|x)} \right]$$
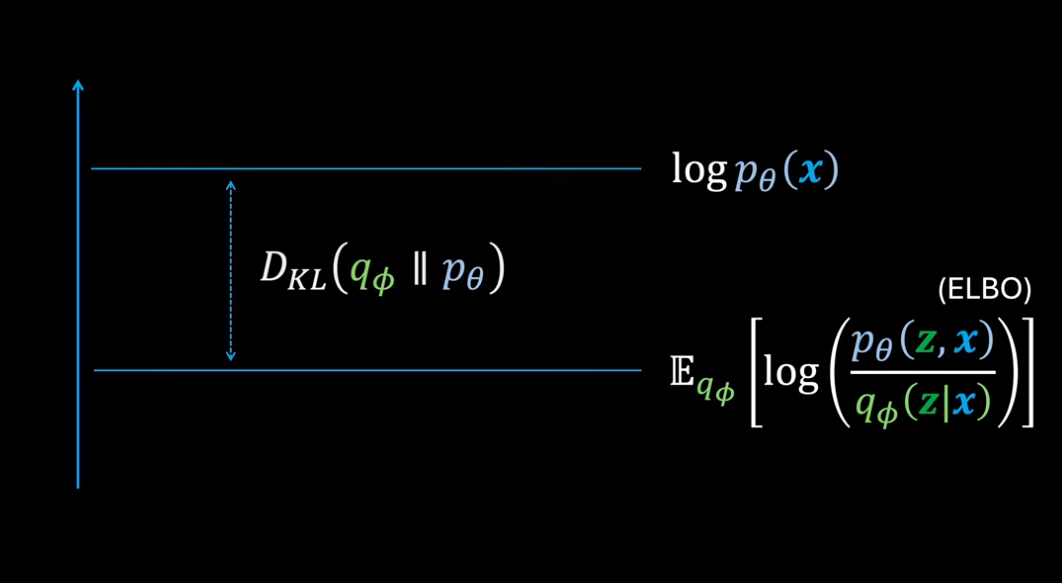
ELBO 还可以从另一个角度,使用琴生不等式进行推导。
$$
\begin{aligned} \log(p(x)) &= \log \left( \int_z p(x, z) \, dz \right) \\ &= \log \left( \int_z p(x, z) \frac{q(z|x)}{q(z|x)} \, dz \right) \\ &= \log \left( \mathbb{E}_{z \sim q(z|x)} \left[ \frac{p(x, z)}{q(z|x)} \right] \right) \\ &\geq \mathbb{E}_{z \sim q(z|x)} \left[ \log \left( \frac{p(x, z)}{q(z|x)} \right) \right] = \text{ELBO} \end{aligned}
$$
这个角度是看不出和 KL 散度之间的关系的。这里的$q(z|x)$事实上是什么都可以。
VAE 本体
VAE 的出发点是最大似然估计。即给定一堆数据和一个参数化的模型,只要让$p(x_i; \theta), i=0,1,2,...$都尽可能大,就可以认为模型代表的分布接近于真实图片在概率空间中的分布。
但直接生成图片的难度是比较高的。更合理的做法是先生成一组 latent 变量,然后根据这组 latent 变量来生成图像。比如在生成手写数字的时候,先决定是哪一个数字,倾斜角度如何,画笔的粗细程度,然后再生成可观测的图片。隐变量记为$z$,可观测的图片就是$x$。它们之间存在一个映射来进行生成,实际上就是 VAE 的 decoder。
关于这个 decoder,还有一些讨论。我们完全可以假设$z arrow x$的映射是确定性的,即$f_\theta (z) = x$,但这样做有一些坏处,后面会看到。实际上使用的是一个随机性的映射,我们假定它是$x|z \sim \mathcal N(f_\theta (z), \sigma^2I)$。此时,decoder 部分完成的实际上是将一个分布映射到另一个分布,并且一个分布中的某个值是随机性地对应于另一个分布中的某个值。这里我们规定了$p_\theta (x|z)$的形式,自然还会有$p_\theta (z|x)$。它可以写成这种形式,是因为这个映射被$\theta$唯一地确定,但这个分布是写不出来的。它也是之后被估计的对象。
$p(x|z)$是被假设的。事实上,只要它的 PDF 是连续的,任意假设都可以在理论推导中成立。我们也可以把确定性的映射当成随机映射的一种特殊情况,即 PDF 是一个 Delta 函数。
另外,我们还需要知道$p(z)$。我们假定$z \sim \mathcal N(0, I)$。苏剑林的解读中认为这个假设并不重要,但实际上确实做了这样一个假设,只不过这个假设是合理的。无论真实的 latent 变量是如何分布的,任意形式的分布总可以正态分布的变换得到。可以认为,decoder 中的前几层学习了从正态分布到潜变量分布的变换,后几层学习了$f_\theta$。
回到学习的目标上。现在,生成一个$x$的过程被拆成了两步。那么就有
$$
p(x_i; \theta)=\int_z p(x_i|z)p(z)dz
$$
尽管不是同一个出发点,但是我们回到了 VI 的核心问题,就是这个积分无法高效地求解。
如果我们能够拿到$p_\theta (z|x)$的解析形式,又会怎么样呢?
$$
p_\theta (x_i)=\frac{p_\theta (x_i|z)p(z)}{p_\theta (z|x_i)}
$$
右边所有的东西都有了解析形式,那左边自然也就算出来了,可以优化了。所以我们是希望拿到$p_\theta (z|x)$的,但这做不到。事实上,我们对生成(generate)的过程作了假设,使得$z$和$z arrow x$的过程都很容易,这就使得$x \rightarrow z$的过程很难求解。VAE 和 DDPM 中都有这种直觉。
这里是在给使用 VI 找理由。事实上,最后优化的目标和这个式子没什么关系。文中找了另外一个借口,即为了在更小的范围而不是整个$z \sim \mathcal N(0, I)$上进行积分而去估计$p(z|x)$,但这和后面实际计算的东西也没有什么关系。实际上只要用一下 VI,就能看到优化的目标了,这里只是找一个动机。
于是我们试图使用一个简单的分布$q_\Phi (z|x)$来替代复杂的$p_\theta (z|x)$,并进行 VI:
$$
\begin{aligned} \text{KL}(q_\Phi(z|x_i) \parallel p_\theta(z|x_i)) &= \mathbb{E}_{z \sim q_\Phi(z|x_i)} \left[ \log \left( \frac{q_\Phi(z|x_i)}{p_\theta(x_i, z)} \right) \right] + \log(p_\theta(x_i)) \\ \log(p_\theta(x_i)) - \text{KL}(q_\Phi(z|x_i) \parallel p_\theta(z|x_i)) &= \mathbb{E}_{z \sim q_\Phi(z|x_i)} \left[ \log \left( \frac{p_\theta(x_i, z)}{q_\Phi(z|x_i)} \right) \right] \end{aligned}
$$
此时,在左侧已经出现了目标,带上一个附加的 KL 散度项。我们希望把左侧整体作为一个目标,使它越大越好。LHS 越大,原来作为目标的对数似然概率就越大,同时 KL 散度越小,代表估计分布$q_Phi$越接近真实分布。右侧是 ELBO,我们尝试计算它:
$$
\begin{aligned} \mathbb{E}_{z \sim q_\Phi(z|x_i)} \left[ \log \left( \frac{p_\theta(x_i, z)}{q_\Phi(z|x_i)} \right) \right] &= \mathbb{E}_{z \sim q_\Phi(z|x_i)} \left[ \log \left( \frac{p_\theta(x_i|z) p_\theta(z)}{q_\Phi(z|x_i)} \right) \right] \\ &= \mathbb{E}_{z \sim q_\Phi(z|x_i)} \left[ \log(p_\theta(x_i|z)) \right] - \text{KL}(q_\Phi(z|x_i) \parallel p(z)) \end{aligned}
$$
- 右侧第二项是$(\theta, x)$的函数。由于两个分布都有解析解,所以它有解析形式。
- 左侧第一项是$(\Phi, z)$的函数。要求在整个分布上求期望,但是在一次推理中,我们只会随机采样一个$z$。于是我们仅用这一个$z$算出的值来代表期望,并希望在多次训练后能够回到它的期望。
这是随机梯度估计的内容,常见于强化学习和各类变分推断的应用场合。这里的核心实际上是期望和求导操作能否对换。
实际上,随机梯度下降本身就是随机梯度估计的一种。我们实际上期望了
$$
\nabla_\theta (\mathbb E_{x \sim D}\left[ \mathcal L(x)\right]) \approx \mathbb E_{x \sim D}[\nabla_\theta \mathcal L(x)]$$这里期望表现为求平均。LHS 是原始的概念上的梯度下降,RHS 是实际上使用的 minibatch。
所以,我们实际上优化的目标是
$$\mathbb{E}_{z \sim q_\Phi(z|x_i)} \left[ \log \left( \frac{p_\theta(x_i, z)}{q_\Phi(z|x_i)} \right) \right] \approx \log(p_\theta(x_i|z)) - \text{KL}(q_\Phi(z|x_i) \parallel p(z))$$
注意到第一项是$(\Phi, z)$的函数,但$z$无法将梯度继续传给上一层,这里会使用 reparameterization trick。这不是重点,这里略过。
这里在考虑计算梯度时,已经可以看到不能在$p_\theta (x_i|z)$上使用确定性模型的理由。此处在求导是必然要求 PDF 可导,确定性模型显然是不行的。
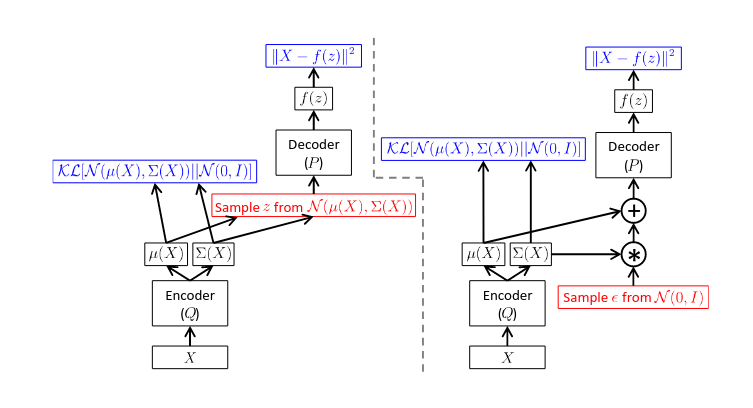
接下来就可以把之前的假设代入,获得真实的 loss:
$$
p_\theta(x_i|z) = \frac{1}{\sqrt{2\pi}\sigma} \exp \left( -\frac{1}{2\sigma^2} (x_i - f_\theta(z))^2 \right),
$$
$$
\text{KL}(q_\Phi(z|x_i) \parallel p(z)) = \sum_{i=1}^d \left( \mu_i^2 + \sigma_i^2 - \log(\sigma_i^2) - 1 \right)
$$
其中第二个式子中使用的是 latent 空间中 encoder 算出的均值和方差的分量。ELBO 是需要最大化的,将两侧同时取反,变为常用的最小化目标。忽略其中所有的常数项,得到优化目标
$$
\text{Loss} = \frac{1}{2\pi \sigma^2} (x_i - f_\theta(z))^2 + \sum_{i=1}^d \left( \mu_i^2 + \sigma_i^2 - \log(\sigma_i^2) - 1 \right)
$$
其中第一项实际上是重构误差,第二项的含义是让每一个样本的$p(z|x_i)$都靠近$\mathcal N(0, I)$。一方面可以从 KL 散度的含义看出来,另一方面可以将后一项 loss 拆成$(\mu_i^2)+(\sigma_i^2-\log(\sigma_i^2)-1)$。理想情况下,前后两项都下降为 0,此时前一项得到$\mu_i=0$,后一项得到$\sigma_i^2=1$。苏剑林的解读中认为这一项在计算建模中的意义是防止模型将$\sigma^2$调整成 0 从而退化到 auto encoder,同时保持模型的生成性质,即从$\mathcal N(0, I)$中采样可以对应到所有的图像。






Comments NOTHING