众所周知,LLM 的激活值因为异常值的存在而难以量化。2022年的时候,SmoothQuant 提出使用一个可调节的系数矩阵将量化难度在激活值与权重之间转移,开了该类方法的先河,实现了比较好的 W8A8 动态量化。一年后,OmniQuant 继承了这一思路,把 SmoothQuant 的思想发挥到极限,并通过逐层微调量化相关参数的方式,实现了 W4A4 的动态量化。在此期间,也出现了其他路径的后训练量化方式,例如拆分异常值通道并进行重组(QLLM),又或者利用 FP4 实现更好的量化范围。由于我更关注对硬件的适配性,这些方法显然对硬件不是那么友好,所以就没有关注。
以上方法在 4bit 精度下,均使用了 per-token 的量化方式,并且还是动态量化。这意味着量化参数不能够提前算出并融合到权重中,即会在计算时引入额外的开销。对我来说更困扰的实际上是会改变一些计算流的性质。直到去年,出现了一些新的声音。一种想法抛弃了使用乘性的缩放因子来抑制异常值的做法(指SmoothQuant),转而使用旋转矩阵对激活值和权重进行变换,从而减缓异常值。另一种想法发现了 attention sink 的现象,即特定的 token 上总是会出现异常值,提出了有关 softmax attention 中异常激活值是如何形成的假说,并借用相关的手段吸引异常值的火力。通过结合这两种想法,PrefixQuant 实现了 4bit、per-tensor 且静态的激活值量化,所以今天的主角是它。它是基于 QuaRot 的,所以这里也提到了 QuaRot。
PrefixQuant 被 ICLR 2025 拒收了,主要的原因似乎是 novelty 不够,通过 prefix 抑制激活值的思想已经被用过了云云。但是 review 中提到的两篇文章,其中 CushionCache 尚未开源,QFeP 的仓库只有 6 个 star,我觉得哪一个更好使,是谁在真正用心地维护开源实现,不言而喻。
QuaRot
理论上说,QuaRot 的理论依据应该要追溯到 Quip 和 Quip#,但是理论实在看不懂,这里就记录一些实现细节和直观理解。
实现细节
QuaRot 和 SmoothQuant 相同,都是在某些计算中插入一对矩阵来进行变换,但 QuaRot 使用的是一个单位正交矩阵$Q$和它的逆$Q^T$。这样的变换有一个额外的性质,即这样的一对变换可以跨越 RMSNorm 来进行,即
$$\text{RMSNorm}(x)=\text{RMSNorm}(XQ^T)Q.$$
这一点很容易通过$||Qx||=||x||$的性质进行验证。
QuaRot 使用的矩阵的基础是 Walsh-Hadamard 变换矩阵,即
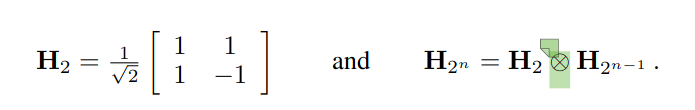
它是一个单位正交阵,标绿的算子代表克罗内克积。QuaRot 在此基础上,对每一行随机地乘上 1 或者 -1,即乘上一个由${1, -1}$构成的对角矩阵。容易验证这也是一个单位正交矩阵,因为这个操作既不会改变行向量的长度(单位长度),也不会改变行向量之间的正交性。
借助这种变换形式,QuaRot 在一层 Transformer 中进行了四次变换:
- 在两次 RMSNorm 处,分别进行了一次变换。即 RMSNorm 前/后的权重分别右乘/左乘了矩阵$Q$及其转置。这保证了通过 RMSNorm 的激活值能够被直接量化。
- 在 $QK^T$ 处,进行了在线的 Hadamard 变换,利用 $(QH)(KH)^T=Q(HH^T)K^T=QK^T$ 进行抵消。此处的变换没有融合到权重中,因为它的前面还有一层 RoPE。这保证了参与 attention 运算的 $Q$ 和 $K$ 都可以被量化。但是在 QuaRot 的代码中似乎只量化了 $K$,我还没看出来是为什么。
- 在 $W_V$ 和 $W_O$ 之间,再进行一次在线的 Hadamard 变换。这个变换是最复杂的一步。
对于 $V$ 的值,QuaRot 选择了先对每个 head 进行 Hadamard 变换,即
$$W_V\leftarrow W_V(I_{n_h}\otimes H_{d_h})$$
但是,QuaRot 希望最终的变换是$H_{n_h\times d_h}$,所以额外利用了恒等式
$$H_{n_h\times d_h}=(I\otimes H_{d_h})(H_{n_h}\otimes I)$$
在 $W_V$ 上,它只融合了前半个矩阵,后半个矩阵在通过了 attention 的计算流程,拼接所有 head 之后,对 $W_O$ 的输入进行量化之前,才进行在线的计算。至于 $W_O$ 的变换,则是直接使用了 $W_O\leftarrow HW_O$。代码中对于在线计算 $Z=Z(H_{n_h}\otimes I)$ 的实现是:
x = fast_hadamard_transform.hadamard_transform(x.reshape(-1, init_shape[-1]//self.had_dim, self.had_dim).transpose(1, 2), scale=1/math.sqrt(init_shape[-1]//self.had_dim)).transpose(1, 2)
其中had_dim就是 head 的特征数,init_shape指的就是[B, T, d]。说实话这个也还没看懂。
目前也没明白为什么 QuaRot 要执着于将最终的变换设置为$H_{n_h\times d_h}$,也不明白这两步为什么非得分开算。这可能就只有实验之后才知道了。
直观理解
这里面最反直觉的一件事情就是,凭什么使用一个随机化的正交矩阵作用在激活值上之后,它就变得容易量化了?
我没有去看理论上的分析,但我觉得有一个偏直觉的解释。随机 Hadamard 变换矩阵是一个单位正交矩阵,这也就意味着它对每一个 token 向量都进行了(镜面的)旋转变换。由于固定的通道中存在异常值,每一个 token 的向量表征在几何空间中都应该是一个非常贴近某个坐标轴的向量。这时,即使是随便施加一个旋转,都很容易缩小各个维度坐标值之间的差距,在二维的情形下可以很容易感受到。
所以理论上应该存在一个旋转,使得各个 channel 之间的值分布基本趋于一致,也就是最优的旋转?我觉得这还是一个有待挖掘的问题
PrefixQuant
outlier 形成假说
在描述 PrefixQuant 的细节之前,我认为有必要提到这个假说,它来自于Quantizable Transformers。这篇文章中观察到异常高的激活值往往出现在无实义的 token 中,例如[SEP]。它认为,outlier 的训练过程中的出现可能经历了以下过程:
- 对于某个 head,它在某个任务中不想对当前的输入附加任何信息,即它希望 Transformer block 输出一个 0 附加到残差连接上。
- 为了实现这一点,它有可能会给这些无实义的 token 学习到很小的 value 值(因为这些 token 本来也就没什么用),然后在不希望附加任何信息时,将所有的 attention 集中到这些 token 上。此时,其他的 token 得不到注意力,因此输出接近于 0;而无实义的 token 得到了注意力,但是它的 value 很小,因此输出也是 0。这就实现了它的目的。
- 那么,如何让注意力集中到无实义的 token 上呢?注意到 softmax 注意力的分配事实上依赖于 token 之间的距离,而非 attention map 值的绝对大小(参考 softmax 的数值稳定计算是比较显然的),并且 softmax 事实上永远不可能表达注意力为 0 和 1 两个值。为了实现上面的效果,即注意力集中到少数 token 上,token 之间的值就必须拉得很远。于是就形成了异常值。
Quantizable Transformers 为了验证这个假设,使用改版的 softmax 替换了原来的 softmax。改版简单来说,就是把 softmax 的上下限拉宽一些,然后截止到$[0, 1]$的范围内,这样它就可以严格表达 0 和 1 了。它发现这样做之后,训练出来的 Transformer 确实量化难度小了。当然,这样做可能也未必很合适,毕竟 softmax 不是 hardmax 的一个原因就是处处可导。文中的模型只有 100M+ 的参数级别,或许再大一些就不好使了?
从这个角度出发,PTQ 之所以变得越来越难,也未必是因为过度训练耗尽了可用的 bit 位数,还有可能是 Transformer 架构自身的原因。
实现细节
PrefixQuant 利用了这一点,并选择在后训练阶段来处理这件事,而非重新训练一个模型。它选择在句子的前面加上几个无实义的 token 来吸引火力,从而降低后续 token 的量化难度。在实现中,这些 token 被提前存入 kv cache 中,并且是全精度的。
实现上其实没什么细节,理解了past_key_value的机制就没什么了。PrefixQuant 是对 QuaRot 的基础上再做了 prefix 的事情,附加传统艺能的逐层微调。代码和 QuaRot 也是差不多的。






Comments NOTHING